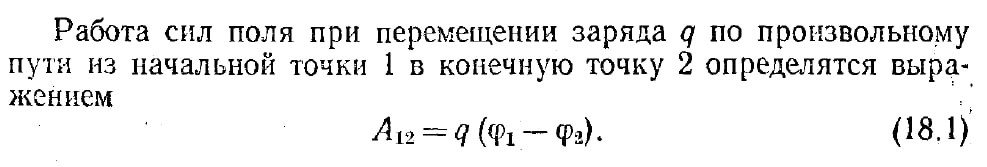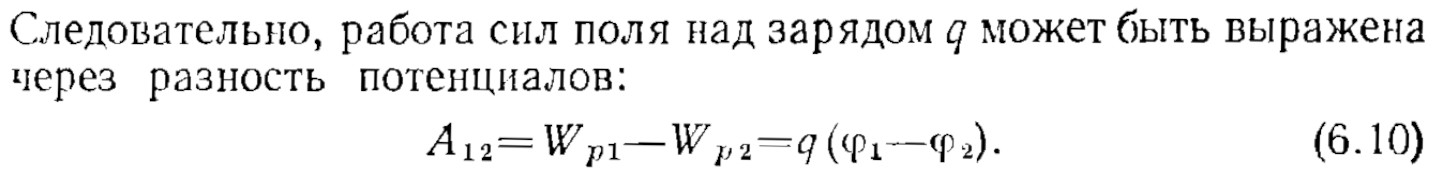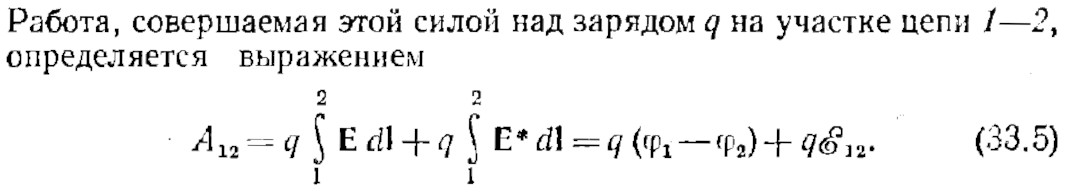Математическая модель — не материальный объект физического мира
В этой части:
- почему электрическая схема не вполне отражает реальность,
- что называют “напряжением” в электродинамике,
- что называют “напряжением” в теории цепей,
- закон Ома — разный для электродинамики и для теории цепей,
- что и как измеряет вольтметр.
Вводный курс, определяющий термины и концепции, которые будут использоваться при дальнейшем анализе.
Теория электрических цепей
Теория электрических цепей работает не с реальными устройствами, а с абстракцией, математической моделью, все процессы в которой характеризуются численными параметрами, называемыми токами и напряжениями. Эти параметры не имеют прямого физического смысла, так как любые явления реального мира, включая электромагнитное взаимодействие и движение носителей заряда, лежат за пределами теории цепей. Поведение элементов в модели описываются исключительно математически.

Справа (схема и нетлист): математическая модель, которая подчиняется законам теории цепей.
В теории линейных электрических цепей всегда справедливы теорема о суперпозиции, два правила Кирхгофа, теоремы об эквивалентных преобразованиях цепей с источниками (Нортон, Тевенен), теоремы о преобразованиях “контур-звезда” (или, в частном случае, “треугольник-звезда“). К моделям электрических цепей применимы методы “узлового” и “контурного” анализа. Высокочастотные модели в теории цепей описывают также в терминах S-параметров.
Элементы в модели электрической цепи соединяются друг с другом с помощью абстрактных проводников. По определению, если две (или более) точки в модели электрической цепи соединены, они в любой момент времени обладают одинаковым параметром “напряжения”.
В отличие от проводников в реальном мире, соединения в модели электрической цепи не имеют геометрических размеров, не обладают свойствами проводимости, индуктивности и ёмкости, не создают электромагнитное поле и не чувствительны к нему.
Электрическая схема — это графическое изображение модели электрической цепи, подчиняющейся аксиомам и теоремам теории цепей, и состоящей из идеализированных элементов и соединений. Схема не отражает физическую структуру реального устройства, взаимное расположение его компонентов и проводов, и является всего лишь одним из способов представления модели электрической цепи. Другой способ представления этой модели — текстовый список соединений, или нетлист, который используется в системах компьютерной симуляции моделей электрических цепей (например, SPICE) и системах автоматизированного проектирования электроники.
Реальное устройство описывается моделью электрической цепи неточно. Это связано с тем, что аксиомы, на которых построена теория цепей, в общем случае не справедливы для реального мира, а идеализированные модели элементов лишь в некотором приближении описывают их реальные прообразы.
В мире электрических схем проблемы земляных петель не существует. У всех соединённых на схеме выводов элементов по определению всегда одинаковое напряжение, а сами соединения не имеют геометрических и физических свойств и не взаимодействуют с электромагнитным полем. Реальные устройства, в отличие от схем, состоят из материальных компонентов и проводников, которые подчиняются законам физики, а не законам теории цепей.
Теорию цепей можно использовать для анализа реальных устройств, если построить более точную модель. Свойства реальных компонентов и проводников, а также взаимодействие электромагнитных полей между ними можно учесть, добавив в модель дополнительные “паразитные” элементы и их связи: сопротивления, ёмкости, индуктивности и коэффициенты взаимной индуктивности. Важно понимать, что у любой модели есть ограничения применимости, и не расценивать её как безусловно точное отражение физической реальности.
Грамотное построение подобных моделей требует понимания фундаментальных физических процессов в реальных устройствах.
Формулы в статье записаны в СИ.
Электромагнитное поле
Электромагнитное взаимодействие — одно из четырёх фундаментальных взаимодействий, помимо гравитационного, сильного и слабого. По современным представлениям, оно осуществляется через электромагнитное поле.
Электрический заряд $q$ — величина, которая определяет способность участвовать в электромагнитном взаимодействии. Электрическим зарядом обладают некоторые элементарные частицы (и это их неотъемлемое свойство); электрическим зарядом может обладать некоторый объём в пространстве (тогда говорят о суммарном электрическом заряде в этом объёме). Если суммарный положительный заряд в выбранном объёме в точности уравновешивает отрицательный, говорят, что этот объём электрически нейтрален (полный заряд равен нулю).
Одним из основополагающих законов физики является закон сохранения электрического заряда. Согласно нему, электрический заряд внутри объёма, границу которого не пересекают носители заряда, не меняется. Внутри могут “рождаться” и “умирать” электрические заряды, но всегда только парами: на каждый отрицательный заряд приходится точно такой же положительный. Суммарный заряд может измениться, только если носители заряда покинут этот объем или, наоборот, попадут в него из внешнего мира.
Электромагнитное поле можно охарактеризовать с помощью силовых и энергетических величин.
Силовые характеристики включают в себя векторы напряжённости электрического поля $\vec E$ и индукции магнитного поля $\vec B$. Эти векторы определяют в каждой точке пространства с помощью понятия векторного поля. Поле вектора $\vec E$ называют электрическим полем, а поле вектора $\vec B$ — магнитным. Электрическое и магнитное поле характеризуют силу, действующую на заряженную частицу со стороны электромагнитного поля (силу Лоренца): $\vec {F} =q(\vec {E} +[ \vec {v} \times \vec {B} ] )$.
Энергетические характеристики включают в себя скалярный потенциал $\varphi$, который ещё называют электрическим потенциалом, и векторный потенциал $\vec A$. Они тоже определяются в каждой точке пространства.
Для описания электромагнитного поля в среде, отличной от вакуума, вводят несколько дополнительных векторов:
- вектор $\vec D$, который определяют как сумму векторов напряжённости электрического поля и поляризации вещества: $\vec D = \varepsilon_0 \vec E + \vec P$,
- вектор $\vec H$, который определяют как разность векторов напряжённости магнитного поля и намагниченности вещества: $\vec H =\frac{1}{\mu_0} \vec B – \vec M$.
Физические свойства электромагнитного поля и его связь с зарядами и токами в полной мере описываются четырьмя уравнениями Максвелла и выражением для силы Лоренца, использующими эти величины.
Четыре уравнения Максвелла могут быть записаны в разных формах, и их интерпретация будет несколько различаться. Для дифференциальной формы смысл следующий:
- закон Гаусса: электрический заряд является источником поля $\vec D$
- закон Гаусса для магнитного поля: магнитные заряды не обнаружены
- закон индукции Фарадея: изменение магнитного поля $\vec B$ порождает вихревое электрическое поле $\vec E$
- теорема о циркуляции магнитного поля: электрический ток и изменение вектора $\vec D$ порождают вихревое магнитное поле
Электрический ток
Электрическим током называют упорядоченное движение носителей электрического заряда. Более обобщённо, это процесс переноса электрического заряда через некоторую воображаемую поверхность в пространстве.
Количественной характеристикой электрического тока является скорость переноса заряда через заданную поверхность в пространстве, или сила тока: $I = dq/dt$. Электрический ток в пространстве можно описать через векторное поле плотности тока $\vec j$, которая равна скорости переноса заряда через элементарное малое сечение $\vec {ds}$. Тогда сила тока через некоторую поверхность выражается как интеграл $ I = \int_S {\vec j \cdot \vec {ds} }$.
Сила и плотность тока не описывают точный механизм переноса электрического заряда. Одна и та же плотность тока может быть обусловлена как движением носителей положительного заряда, так и противоположным по направлению движением отрицательных носителей. Исторически за положительное направление электрического тока принимают направление (реального или эквивалентного) перемещения положительных носителей заряда.
Согласно фундаментальному закону сохранения электрического заряда, скорость изменения заряда в некотором объёме равна алгебраической сумме токов (с учётом знака), втекающих в этот объём:
$$ \frac{dq}{dt} = \sum I_i = \oint_S \vec j d \vec s$$
Важный вывод из этого закона можно сделать для частного случая стационарного распределения заряда, когда $dq/dt = 0$: тогда суммарный ток через поверхность, или интеграл плотности тока тоже равен нулю. На этом основано правило Кирхгофа для токов. В общем случае это выражение преобразуется в уравнение непрерывности.
В теории электрических цепей параметр силы тока можно считать аналогичным физическому понятию силы тока.
Силы, действующие на носители заряда
Все силы, которые действуют на носители заряда, можно условно разделить на три категории:
- кулоновские (“электростатические”),
- диссипативные,
- внешние (“сторонние”).
Кулоновские силы обусловлены электрическим полем стационарного (неизменного во времени) распределения электрического заряда в пространстве. Такое электрическое поле называют стационарным, а его вклад в суммарное поле $\vec E$ называют кулоновской компонентой поля $\vec E_{кул}$. Стационарными являются, например, электростатическое поле (порождённое неподвижными носителями заряда) и поле постоянных токов (порождённое движущимися носителями при условии неизменной плотности заряда в пространстве).
Диссипативные силы иллюстрируют переход механической энергии носителей заряда в другую форму, обычно — в тепловую энергию. Их направление противоположно средней дрейфовой скорости носителей заряда. Величина диссипативных сил зависит от этой скорости и не пропорциональна величине заряда, поэтому их не представляют как компоненту поля $\vec E$. Чаще всего эти силы скрываются внутри других понятий, таких как удельная проводимость.
Все остальные силы, действующие на носители заряда (кроме кулоновских и диссипативных), называют внешними. В отличие от кулоновских и диссипативных сил, внешние силы способны перемещать носители заряда против направления действия кулоновских сил, и таким образом поддерживать электрический ток. Их влияние на носитель заряда может быть представлено в виде второй компоненты поля $\vec E_{вн}$.
Итоговое поле $\vec E$ является суперпозицией компонент кулоновских и внешних сил: $\vec E = \vec E_{кул} + \vec E_{вн}$. Напряжённость поля $\vec E$ определяет силу, действующую на носитель заряда со стороны электрического поля $\vec F_E = q \vec E$.
Разность потенциалов
Электрическое поле $\vec E$ обладает свойством потенциальности, если работа сил этого поля, действующих на пробный заряд при его перемещении по любой замкнутой траектории равна нулю. Обычно подразумевают, что во время этого перемещения поле остаётся неизменным. На математическом языке потенциальность поля означает, что ротор поля в любой точке равен нулю, или что его циркуляция по произвольной траектории равна нулю. Для потенциального поля существует скалярная функция потенциала, градиент которой равен величине поля в каждой его точке.
В физике используется величина $\varphi$, противоположная математической функции потенциала по знаку. Она отражает энергетический смысл потенциала силового поля, в котором положительная работа сил поля приводит к убыли потенциальной энергии: $\vec F = – \mathrm {grad}\ W_{pot}$. Для потенциального электрического поля величина $\varphi$ называется скалярным электрическим потенциалом, и $\vec E = – \mathrm {grad}\ \varphi$.
Традиционно понятие потенциала (электростатического потенциала) в курсе физики вводится для электростатического поля, но оно применимо к любому потенциальному полю, например, электрическому полю постоянных токов. Электрическое поле, порождённое движущимися носителями при условии неизменной плотности заряда в пространстве, стационарно (не меняется во времени) и потенциально.
Электрическое поле $\vec E = \vec E_{кул} + \vec E_{вн}$ в общем случае состоит из двух компонент, одна из которых ($\vec E_{вн}$) не потенциальна. Поэтому, когда говорят о потенциале поля $\vec E$, подразумевают именно кулоновскую компоненту $\vec E_{кул}$. Важно понимать, что в общем случае электрическое поле $\vec E = \vec E_{кул} + \vec E_{вн}$ не является потенциальным, даже если оно стационарно.
Разность потенциалов между точками 1 и 2 определяют как разность удельной потенциальной энергии пробного заряда в поле $\vec E_{кул}$ в этих точках:
$$\varphi_1 – \varphi_2 = \frac{1}{q_{пр}} (W_{pot\_1} – W_{pot\_2})$$
Также разность потенциалов можно выразить через работу сил поля $\vec E_{кул}$ по перемещению пробного заряда из одной точки в другую:
$$\varphi_1 – \varphi_2 = \int_1^2 \vec E_{кул} d \vec l$$
В качестве примера можно рассмотреть потенциал и напряжённость электрического поля $\vec E = \vec E_{кул}$ вдоль проводника с постоянным током, состоящего из отрезков с разной проводимостью:
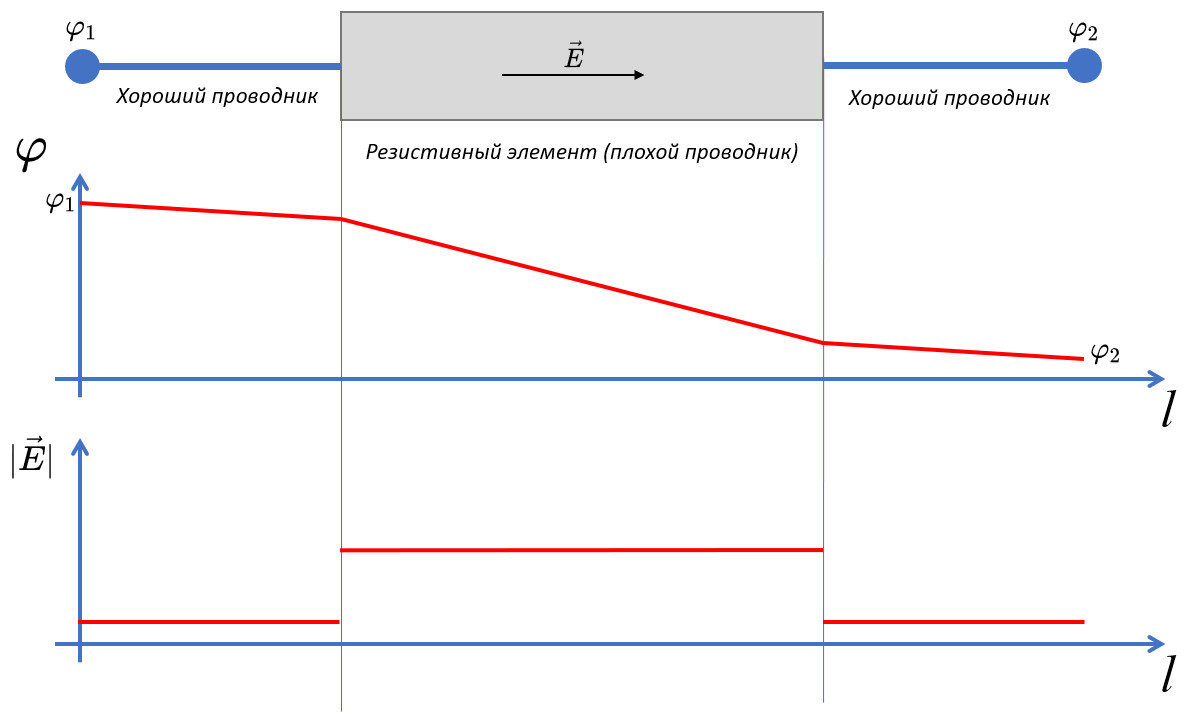
Хотя разность потенциалов и определяется через кулоновскую компоненту поля, было бы ошибкой сказать, что на неё не оказывают влияние внешние силы. Дело в том, что само распределение электрического заряда в пространстве, которое определяет напряжённость кулоновской компоненты поля, может быть сформировано под воздействием внешних сил.
Постоянный ток в изображённом проводнике поддерживается источником ЭДС (который не показан), и внешние силы действуют строго внутри источника. Распределение заряда в проводнике было бы совершенно другим в отсутствие внешних сил несмотря на то, что они действуют только в пределах источника ЭДС и не влияют непосредственно на носители заряда в этом проводнике.
Для электрического поля переменного тока существует квазистационарное приближение. Если ток смещения в проводниках пренебрежимо мал в сравнении с током проводимости, а вне проводников плотность тока равна нулю, поле переменного тока можно считать стационарным в каждый отдельный момент времени. Эти условия преобразуются в выражение $\omega \ll \tilde {c} / l$, где $\omega$ — угловая частота тока, $\tilde {c}$ — скорость света в диэлектрике, окружающем проводник, $l$ — размер области, для которой определяют критерий квазистационарности. Грубая оценка предела применимости этого приближения для участка печатной платы размером 5 см даёт максимальную частоту около ~100 МГц.
ЭДС
Ранее мы описывали внешние силы в терминах компоненты электрического поля $\vec E_{вн}$. Для них также существует скалярная энергетическая характеристика в виде электродвижущей силы, или ЭДС ($\mathcal {E}$).
Исторически принятый термин не вполне корректен. С физической точки зрения и по размерности ЭДС — это не сила, а мера удельной энергии или работы (вольт = Дж/Кл)
ЭДС определяется как удельная работа внешних сил по перемещению пробного заряда между двумя точками по заданной траектории: $\mathcal {E}_{12} = A_{вн\_12} / q_{пр}$. Через компоненту электрического поля $\vec E_{вн}$, обусловленную внешними силами, ЭДС выражается как интеграл
$$\mathcal {E}_{12} = \int_1^2 \vec E_{вн} d \vec l$$
В зависимости от выбора точек и траектории интегрирования, можно говорить об ЭДС на участке цепи, ЭДС источника или об ЭДС в замкнутом контуре. В отличие от кулоновских (потенциальных) сил, работа внешних сил зависит от выбора траектории, а циркуляция не равна нулю. Другими словами, в общем случае ЭДС между двумя точками в пространстве не определена однозначно.
Электрическое поле внешних сил $\vec E_{вн}$ может порождаться как неэлектрическими процессами (химические, тепловые, диффузионные, … ), так и изменяющимся во времени магнитным полем, что называется явлением электромагнитной индукции.
ЭДС сосредоточенных источников
Для многих источников ЭДС поле внешних сил $\vec E_{вн}$ можно считать потенциальным в пределах внутреннего объёма, ограниченного поверхностью источника. Тогда при выборе траектории между клеммами, целиком лежащей внутри источника, величина ЭДС определяется однозначно.
Традиционно под значением ЭДС источника понимают положительную величину, равную удельной работе внешних сил по переносу положительного заряда от отрицательной клеммы к положительной при условии выбора траектории переноса, целиком проходящей внутри источника.
Электрическое напряжение
Термин один, понятия — разные
Электрическое напряжение (или просто напряжение) — редкий случай физического термина, которому в разных источниках присваивают как минимум два принципиально разных определения:
- напряжение равно разности потенциалов
- напряжение не равно разности потенциалов в общем случае, и выражается через суммарную удельную работу кулоновских и внешних сил
Также существуют учебники и книги по физике, которые не определяют понятие напряжения в явном виде, или присваивают ему произвольный смысл в разных местах по тексту.
Первый подход приравнивает напряжение к разности потенциалов. В электростатике, при условии отсутствия внешних сил, удельная работа кулоновских сил (разность потенциалов) действительно равна полной удельной работе электрического поля, но в общем случае это не так. Приведённое определение противоречит ГОСТ Р 52002-2003, Большой Российской Энциклопедии и большинству классических книг по электродинамике.
Второй подход выделяет напряжение как самостоятельное физическое понятие, и определяет его как полную удельную работу электрического поля $\vec E = \vec E_{кул} + \vec E_{вн}$. Он будет описан далее как “напряжение в электродинамике”.
Напряжение в электродинамике
Суммарная удельная работа кулоновских и внешних сил по перемещению пробного заряда из одной точки в другую по выбранной траектории называется электрическим напряжением между этими точками. Поскольку в эту сумму входит работа внешних сил, которая зависит от траектории, напряжение в общем случае также зависит от траектории.
$$ U_{12} = U_1 – U_2 = \frac{A_{total}}{q_{пр}} = \frac{A_{кул}+A_{вн}}{q_{пр}} $$
Напряжение можно выразить в терминах компонент напряжённости электрического поля:
$$ U_{12} = \int_1^2 (\vec E_{кул} + \vec E_{вн})d \vec l = \int_1^2 \vec E d \vec l $$
В это выражение вместо интегралов можно подставить разность потенциалов и ЭДС:
$$ U_{12} = \varphi_1 – \varphi_2 + \mathcal {E}_{12}$$
Если на выбранной траектории между точками 1 и 2 не действуют внешние силы, то есть отсутствуют источники ЭДС, напряжение (по этой траектории) равно разности потенциалов: $ U_{12} = \varphi_1 – \varphi_2$.
Напряжение в теории электрических цепей
В теории цепей параметр, называемый напряжением (или потенциалом), однозначно определён для каждого узла (node) модели электрической цепи относительно некоторой точки отсчёта, называемой “узлом нулевого потенциала” или просто “землёй” (ground node). Физический смысл этого параметра аналогичен физическому понятию разности потенциалов между выбранной точкой и землёй цепи.
Второе правило Кирхгофа (или правило Кирхгофа для напряжений) гласит, что для любого замкнутого участка цепи (вне зависимости от выбора “траектории” или “пути обхода”) алгебраическая сумма напряжений на каждом элементе, с учётом направления обхода, равна нулю:
$$ \sum U_i = 0 $$
Второе правило Кирхгофа в терминах разности потенциалов, принятых в физике (как прообраз параметра напряжения в теории цепей), выглядит как определение потенциальности: работа поля $\vec E_{кул}$ между двумя совпадающими точками всегда равна нулю:
$$ \oint \vec E_{кул} d \vec l = 0 $$
В теории цепей, как и в электронике в целом, часто используют понятия “напряжения”, “падения напряжения” и “разности потенциалов” вперемешку, в каждом случае подразумевая именно разность потенциалов. Это неверно с физической точки зрения, но широко распространено в контексте электроники и соответствует бытовому представлению, в котором “напряжение” и “разность потенциалов” – синонимы. Строгое разделение понятий существует, похоже, только в электродинамике.
Закон Ома
Закон Ома как исторический артефакт
В 1825-1827 годах Георг Ом проводил опыты с источником ЭДС в виде термопары, гальванометром и металлической проволокой. Он обнаружил, что сила тока через проволоку в его опытах хорошо описывается линейным законом на основе трёх параметров, и в 1827 году опубликовал результаты.
Величина силы тока в его работе обозначалась S, константы a и b определяли собственные свойства источника, а переменная x соответствовала свойствам подключённого проводника. Эта запись напоминает современный “закон Ома для полной цепи”, но в ней не используются такие физические понятия как ЭДС или сопротивление.

Именно это Георг Ом опубликовал по результатам своих опытов
Работа Ома (1827) была опубликована до зарождения теории цепей и правил Кирхгофа (1847), систем переменного тока (1835-1855), представления об электромагнитном поле (1864), уравнений Максвелла (1884), и, конечно, до теории Друде (1900). Георг Ом проводил опыты и анализировал результаты, не имея возможности дать корректное физическое обоснование наблюдаемым эффектам.
Закон Ома как вывод из теории Друде
Электрический ток в металлах обусловлен направленным дрейфом электронов и описывается в классическом приближении теорией Друде. Эта теория не позволяет предсказать движение какого-то одного конкретного электрона, зато хорошо описывает усреднённые свойства множества электронов в некой макроскопической области.
Основная идея теории Друде заключается в том, что под действием постоянного электрического поля электроны в металлах двигаются с постоянной средней дрейфовой скоростью, пропорциональной напряжённости поля $\vec E$. Согласно второму закону Ньютона ($\vec F = m \vec a$) постоянная скорость, то есть отсутствие ускорения, означает, что существуют другие силы, уравновешивающие $\vec F_E = -e_0 \vec E$. Эти силы называются диссипативными.
Природа диссипативных сил в теории Друде связана со “столкновениями” электронов с ионами кристаллической решётки металла, которые учащаются при росте средней дрейфовой скорости. Работой диссипативных сил объясняется тепловое действие электрического тока. Количественно диссипативные силы в проводниках описывают с помощью параметра удельной проводимости материала $\sigma$ (или обратной величины, называемой удельным сопротивлением $\rho = 1 / \sigma$).
Согласно теории Друде, плотность тока в металлах пропорциональна полной напряжённости поля $\vec E = \vec E_{кул} + \vec E_{вн}$ и удельной проводимости материала $\sigma$. Эту формулу называют дифференциальной формой закона Ома:
$$\vec j = \sigma \vec E$$
Интегральная форма этого выражения для некоторого проводника, в котором действуют кулоновские и внешние силы, называется законом Ома для неоднородного участка цепи:
$$ I R = \varphi_1 – \varphi_2 + \mathcal {E}_{12} $$
$$ I R = U_{12} $$
Именно эту формулу, основанную на теории Друде, чаще всего подразумевают под “законом Ома” в физике. Теория Друде, хотя и не фундаментальна, описывает многие проводящие материалы в достижимом на практике диапазоне напряжённости поля $\vec E$.
Закон Ома в теории цепей
Теория электрических цепей использует комплексные величины для описания переменного напряжения и тока, а также свойств элементов, обладающих ёмкостью и индуктивностью. Определение импеданса как комплексного обобщённого “оператора сопротивления” было введено в 1886 году Оливером Хевисайдом; в 1893 году Артур Кенелли провёл прямую аналогию между концепцией комплексного оператора и векторным представлением импеданса (разработанным Флемингом в 1889), и в том же году Чарлз Протеус Штейнмец обобщил работу Кенелли, представив напряжение и ток также в виде комплексных операторов. Это позволило записать обобщённую форму закона Ома в теории цепей с использованием комплексных операторов:
$$ \hat I = \frac{\hat U}{\hat Z} $$
Этот закон теории цепей определяет связь напряжения $\hat U$ и тока $\hat I$ для сосредоточенного элемента с комплексным импедансом $\hat Z$.
Что измеряет вольтметр

Исторически вольтметр был электромеханическим прибором, который градуировался в вольтах, но при этом фактически измерял силу тока через сравнительно большое внутреннее сопротивление. Угол поворота стрелки был результатом баланса силы упругости возвратной пружины и силы Ампера, пропорциональной току через катушку измерительной головки.
В установившемся режиме распределение заряда стационарно, а значит, ток через клеммы прибора (обозначим их как A и B), измерительную головку и резистор одинаков в силу закона сохранения заряда. Согласно теории Друде, плотность тока в проводниках пропорциональна полному электрическому полю: $ \vec j = \sigma \vec E $. Тогда ток через измерительную головку и показания прибора пропорциональны полю $\vec E$ в её проводниках. Разумно предположить, что внутри вольтметра нет источников ЭДС (работа внешних сил равна нулю), и тогда $\vec E = \vec E_{кул}$, а показания пропорциональны разности потенциалов между клеммами (или напряжению между ними при условии выбора траектории, целиком проходящей внутри вольтметра).

Сегодня вольтметр — электронное устройство, которое чаще всего имеет входной каскад на основе полевых транзисторов с изолированным затвором. Ток через такой вольтметр очень близок к нулю и обусловлен паразитными эффектами, в том числе проводимостью подзатворного диэлектрика входных транзисторов, туннельным эффектом и инжекцией горячих носителей. Типичные современные вольтметры имеют входное сопротивление около $10^7…10^9 \: \Omega$ (десятки – тысячи мегаом), а специализированные электрометры — уровня $10^{16} \: \Omega$ (десятки петаом).
Показания такого прибора определяются напряжённостью электрического поля $\vec E$ в подзатворной области транзисторов, управляющей проводимостью канала сток-исток (более точно, частью этой напряжённости, обусловленной распределением зарядов на затворе и субстрате, то есть без учёта ортогональной напряжённости поля смещения сток-исток). Это поле порождено стационарным распределением зарядов, то есть $\vec E = \vec E_{кул}$.
Поскольку ток через прибор близок к нулю, напряжённость поля в проводах внутри прибора, соединяющих клеммы и транзисторы (как и разность потенциалов на них) тоже близка к нулю. Как и в прошлом примере, предположим, что ЭДС в этих проводах внутри вольтметра отсутствует.
Тогда показания вольтметра пропорциональны разности потенциалов между его клеммами (или напряжению между ними при условии выбора траектории, целиком проходящей внутри него), как и в случае с электромеханическим вольтметром.
Правильный, но не очень полезный ответ на вопрос “что измеряет вольтметр” — разность потенциалов между своими клеммами $\varphi_{AB} = \varphi_A – \varphi_B$, которая при условии выбора траектории, проходящей строго внутри вольтметра, совпадает с напряжением $U_{AB}$.
Вольтметр подключается проводами
Добавим измерительные провода, соединяющие клеммы A и B вольтметра с некоторыми точками 1 и 2 электронного устройства.
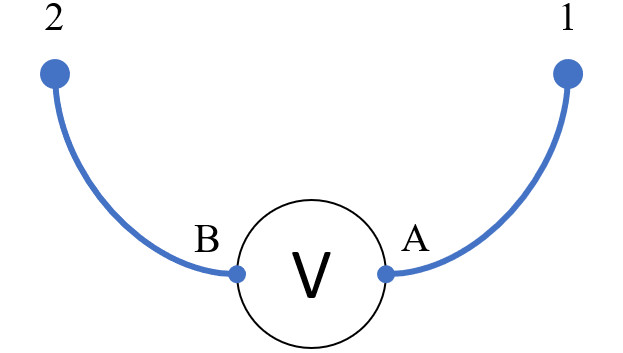
По определению потенциальности $\varphi_1 – \varphi_2$ одинакова для любой произвольной траектории интегрирования. Выберем траекторию, проходящую вдоль проводов и сквозь вольтметр. Тогда $\varphi_{12} = \varphi_1 – \varphi_2$ можно представить как сумму трёх компонент (для сокращения записи использованы двойные индексы):
$$ \varphi_{12} = \varphi_{1A} + \varphi_{AB} + \varphi_{B2} $$
Здесь $\varphi_{AB}$ соответствует показаниям вольтметра, а $\varphi_{1A}$ и $\varphi_{B2}$ — разности потенциалов между концами каждого измерительного провода с учётом знака. Показания вольтметра выражаются как:
$$ \varphi_{AB} = \varphi_{12} – (\varphi_{1A} + \varphi_{B2}) $$
Сумма $\varphi_{1A} + \varphi_{B2}$ определяет расхождение между показаниями вольтметра и фактической разностью потенциалов между точками 1 и 2.
Измерительный провод — это проводник, который хорошо описывается теорией Друде. Помимо кулоновских сил в нём могут действовать внешние силы различной природы: электромагнитная индукция (в присутствии меняющегося во времени внешнего магнитного поля), контактные или термоэлектрические эффекты. Рассмотрим один из проводов (например, 1-A) подробнее. Выразим разность потенциалов между концами провода через закон Ома для неоднородного участка (с учётом действия внешних сил):
$$ \varphi_{1A} = IR – \mathcal {E}_{1A} $$
Слагаемое $IR$ чаще всего пренебрежимо мало. Ток определяется напряжением $U_{12}$ (по траектории через вольтметр) и входным сопротивлением вольтметра, которое для любого современного прибора имеет порядок 1 МОм и более. Сопротивление измерительных проводов обычно меньше 1 Ома. Тогда при измерении разности потенциалов в 10 вольт вклад слагаемого IR в одном проводе будет меньше 0.01 мВ (без учёта эффекта “нагрузки” источника разности потенциалов), что на несколько порядков меньше погрешности такого вольтметра.
Вклад $- \mathcal {E}_{1A}$ может быть значительно больше, и не уничтожается при бесконечном входном сопротивлении вольтметра. Чаще всего источником ЭДС в проводе является электромагнитная индукция, то есть изменяющееся во времени магнитное поле $\vec B$ (или перемещение провода в стационарном поле $\vec B$). Так, движение провода в поле неодимового магнита может возбудить ЭДС порядка 1 мВ.
C учётом эффектов в измерительных проводах показания вольтметра равны:
$$ \varphi_{AB} = \varphi_{12} – IR_{wires} + \mathcal {E}_{1A} + \mathcal {E}_{B2}$$
$$ \varphi_{AB} \approx \varphi_{12} + \mathcal {E}_{wires}$$
Еще один интересный вывод можно сделать, записав интеграл $\vec E$ по траектории между точками 1 и 2, проходящей сквозь вольтметр и его провода. Этот интеграл равен напряжению между точками 1 и 2 по выбранной траектории.
$$U_{12} = \int_1^2 (\vec E_{вн} + \vec E_{кул}) d \vec l$$
$$U_{12} = \varphi_{1A} + \varphi_{AB} + \varphi_{B2} + \mathcal {E}_{1A} + \mathcal {E}_{AB} + \mathcal {E}_{B2}$$
$$U_{12} =\varphi_{AB} + IR_{1A} – \mathcal {E}_{1A} + IR_{B2} – \mathcal {E}_{B2} + \mathcal {E}_{1A} + \mathcal {E}_{B2}$$
$$U_{12} = \varphi_{AB} + IR_{1A}+ IR_{B2}$$
$$\varphi_{AB} = U_{12} – IR_{wires} $$
$$\varphi_{AB} \approx U_{12}$$
Итак, правильные ответы на вопрос “что измеряет вольтметр” с учётом допущений, что внутри вольтметра (точнее, внутри его измерительной цепи) не действуют внешние силы, а вкладом $IR_{wires}$ можно пренебречь:
- разность потенциалов между своими клеммами $\varphi_{AB}$
- напряжение между своими клеммами $U_{AB}$ (траектория целиком внутри вольтметра)
- напряжение $U_{12}$ между точками, куда подключены его измерительные провода (траектория сквозь провода и вольтметр, 1-A-B-2)
- разность потенциалов между точками, куда подключены его измерительные провода, плюс суммарная ЭДС в этих проводах
Если ЭДС в проводах отсутствует, $\varphi_{AB} \approx \varphi_{12} \approx U_{AB} \approx U_{12}$.
Осциллограф – это быстрый вольтметр, подключаемый к цепи с помощью специального пробника. Для него справедливы все полученные выводы, но следует также учесть влияние свойств щупа. На высоких частотах квазистационарное приближение также может вносить некоторую ошибку.
Напряжение, ЭДС и разность потенциалов в примерах
А теперь — слайды
В рассматриваемых примерах, если явно не сказано иное, для упрощения подразумевается:
- проводимость окружающей среды равна нулю (вне проводников ток не течёт)
- используется квазистационарное приближение (в проводниках доминирует ток проводимости)
- синие провода имеют высокую проводимость $\sigma$ (их сопротивление пренебрежимо мало)
- внешние силы внутри батареи обусловлены только внутренними химическими процессами
- внешние силы внутри резисторов отсутствуют (резисторы маленькие в сравнении с проводами)
- краевыми эффектами (поле около клемм и соединений) можно пренебречь
Все примеры рассматриваются с точки зрения законов физики и теории электромагнитного поля.
Батарейка
Представим себе батарею, лежащую на столе. Внешнее электрическое поле потенциально. Определим положительную клемму как точку 1, отрицательную — как точку 2.
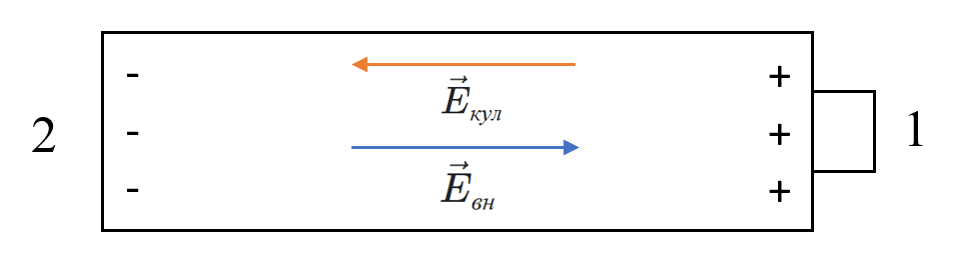
Химические процессы, действующие внутри батареи, перемещают заряженные частицы и создают неравномерное в объёме распределение заряда. Батарея в целом при этом электрически нейтральна, то есть суммарный заряд равен нулю. Интенсивность химических процессов снижается по мере роста градиента заряда, и при достижении некоторого конечного градиента эти процессы прекращаются вовсе. В равновесном состоянии носители заряда имеют нулевую среднюю дрейфовую скорость, на отрицательной клемме батареи (2) скопился некоторый отрицательный электрический заряд, на положительной клемме (1) — такой же по величине положительный.
Действие химических процессов внутри батареи можно описать в терминах компоненты электрического поля $\vec E_{вн}$, порождённой внешними (не кулоновскими) силами. Это поле имеет направление от отрицательной клеммы к положительной, существует только внутри батареи (а снаружи батареи равно нулю) и не потенциально.
Стационарное распределение носителей заряда в пространстве порождает кулоновскую компоненту поля $\vec E_{кул}$, направленную противоположно $\vec E_{вн}$. Суммарная сила, действующая на носители заряда в равновесном состоянии, равна нулю (иначе они бы перемещались), поэтому $\vec E_{кул} = -\vec E_{вн}$ в каждой точке внутри батареи.
Рассмотрим разность потенциалов, ЭДС и напряжение между точками 1 и 2.
Разность потенциалов равна $\varphi_1 – \varphi_2 = \int_1^2 \vec E_{кул} d \vec l$ и положительна, то есть потенциал точки 1 (положительной клеммы) выше, чем точки 2 (отрицательной клеммы). По определению разность потенциалов не зависит от траектории.
Электродвижущая сила равна $\mathcal {E}_{12} = \int_1^2 \vec E_{вн} d \vec l$ и зависит от выбора пути интегрирования:
- Для траектории, целиком проходящей внутри батареи, $\mathcal {E}_{12}$ отрицательна.
- Вне батареи поле внешних сил $\vec E_{вн}$ отсутствует, и $\mathcal {E}_{12}$ равна нулю.
Обычно под значением ЭДС источника понимают величину, полученную при обходе от отрицательной клеммы к положительной, то есть $ \mathcal {E}_{21} = -\mathcal {E}_{12} $, или просто $\mathcal {E}_{бат}$.
Напряжение определено как $U_{12} = \int_1^2 (\vec E_{кул} + \vec E_{вн}) d \vec l$, и зависит от выбора пути интегрирования:
- Для траектории, целиком проходящей внутри батареи, напряжение равно нулю, так как в каждой точке суммарное поле $\vec E_{кул} + \vec E_{вн}$ равно нулю.
- Для траектории вне батареи напряжение равно разности потенциалов, так как внешние силы (и компонента $\vec E_{вн}$) существуют только внутри.
Так как внутри батареи в каждой точке $\vec E_{кул} = -\vec E_{вн}$, разность потенциалов и напряжение (при выборе траектории вне батареи) равны $\mathcal {E}_{бат}$.
Батарейка и вольтметр
Возьмём батарею из прошлого опыта и соединим её с вольтметром.
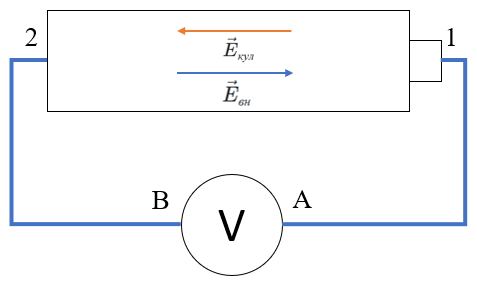
На рисунке изображены почти реальные батарейка, провода и вольтметр.
Вольтметр измеряет разность потенциалов между точками 1 и 2, плюс суммарную ЭДС в измерительных проводах (вкладом $IR$ в проводах можно пренебречь):
$$ \varphi_{AB} \approx \varphi_{12} + \mathcal {E}_{1A} + \mathcal {E}_{B2}$$
Воспользуемся результатами анализа предыдущего опыта, предполагая, что ток через вольтметр (равный току через батарею) пренебрежимо мал. Тогда разность потенциалов между точками 1 и 2 численно равна $\mathcal {E}_{бат}$, а показания вольтметра выражаются как:
$$ \varphi_{AB} \approx \mathcal {E}_{bat} + \mathcal {E}_{1A} + \mathcal {E}_{B2}$$
Внешнее электромагнитное поле, если оно неизменно во времени (а провода неподвижны), не влияет на показания вольтметра, и тогда показания совпадают с ЭДС батареи: $ \varphi_{AB} \approx \mathcal {E}_{bat}$.
Аналогичный результат можно получить, используя электрическое напряжение. Показания прибора равны напряжению $U_{12}$ по траектории, проходящей сквозь провода и вольтметр. По результатам прошлого опыта, при условии потенциальности внешнего электрического поля $U_{12} = \mathcal {E}_{бат}$, так как выбранная траектория целиком лежит вне батареи.
Батарейка, вольтметр и резистор
Теперь рассмотрим соединённые параллельно батарейку, вольтметр и резистор (то есть не очень хороший проводник). В такой цепи существует стационарный (постоянный) электрический ток.
Для удобства анализа будем считать, что носителями заряда в батарее и в резисторе являются положительно заряженные частицы. Тогда направление силы, действующей на них со стороны электрического поля, совпадает с направлением вектора напряжённости поля. Направление средней дрейфовой скорости положительных носителей заряда совпадает с направлением электрического тока. Для отрицательных носителей направление всех сил и дрейфовой скорости изменится на противоположное, но рассуждения останутся корректными.
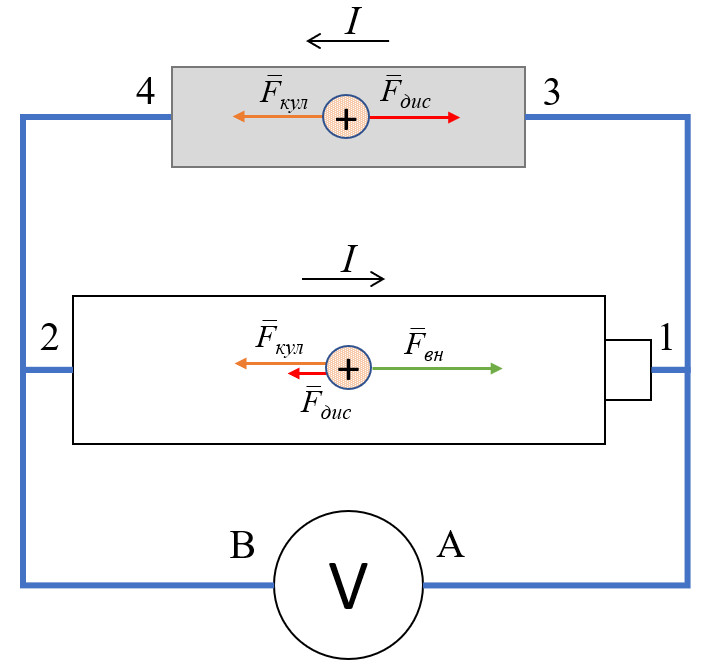
Поскольку сила тока, текущего через вольтметр, пренебрежимо мала, можно считать силу тока через батарею равной силе тока через резистор (закон сохранения заряда). Обозначим её как $I$.
Анализ для батареи
На условный носитель положительного заряда внутри батареи действуют три силы, сумма которых в силу стационарности равна нулю:
- $\vec F_{вн}$, связанная с химической ЭДС батареи и компонентой $\vec E_{вн}$,
- $\vec F_{кул}$, связанная с кулоновской компонентой поля $\vec E_{кул}$ внутри батареи,
- $\vec F_{дис}$, связанная с диссипативными силами внутри батареи.
Направление сил $\vec F_{вн}$ и $\vec F_{кул}$ для условного положительного носителя совпадает с соответствующими напряжённостями $\vec E_{вн}$ и $\vec E_{кул}$. Направление диссипативной силы противоположно средней дрейфовой скорости носителя, и для положительного носителя противоположно направлению электрического тока.
Работа диссипативных сил внутри батареи
В каждой точке внутри батареи силы уравновешены, то есть $\vec F_{вн}+\vec F_{кул}+\vec F_{дис} = 0$
Выразим диссипативную силу: $$ \vec F_{дис} = – \vec F_{вн} – \vec F_{кул} $$
Проинтегрируем это выражение по траектории между точками 1 и 2, проходящей внутри батареи: $$ \int_1^2 \vec F_{дис} d \vec l = – \int_1^2 (\vec F_{кул} + \vec F_{вн}) d \vec l $$
Заменим суммарную работу кулоновских и внешних сил на напряжение (по его определению): $$ A_{дис} = – U_{12} \cdot q_{пр} $$
Разделим обе части на условное время $dt$, за которое совершается перемещение пробного заряда. При этом работа диссипативных сил превращается в мощность, а отношение пробного заряда к времени — в силу тока: $$ A_{дис} / dt = – U_{12} \cdot q_{пр} / dt$$ $$ P_{дис} = – U_{12} \cdot I $$
С учётом того, что ток направлен от точки 2 к точке 1, то есть противоположно выбранному направлению обхода для напряжения, изменим порядок индексов и знак: $$ P_{дис} = U_{21} \cdot I $$
Таким образом мы показали, что мощность диссипативных сил равна произведению напряжения (по траектории, проходящей сквозь область действия диссипативных сил) на силу тока. Это выражение называется законом Джоуля-Ленца и справедливо в любой системе стационарного тока.
Количественной характеристикой диссипативных сил внутри батареи является её внутреннее сопротивление $r$. Тогда, согласно закону Ома для неоднородного участка, $$ U_{21} = I \cdot r $$ Подставим $U_{21}$ в выражение для мощности диссипативных сил, и получим ещё одну популярную (хотя и менее фундаментальную) запись закона Джоуля-Ленца: $$ P_{дис} = I^2 r $$
Запишем разность потенциалов и напряжение между точками 1 и 2 с использованием внутреннего сопротивления $r$, учитывая, что $U_{12} = \varphi_1 – \varphi_2 + \mathcal {E}_{12}$:
$$\varphi_1 – \varphi_2 = U_{12} – \mathcal {E}_{12} = \mathcal {E}_{bat} – I \cdot r $$
Напряжение $U_{12} = \int_1^2 (\vec E_{кул} + \vec E_{вн}) d \vec l$ зависит от траектории интегрирования:
- Для траектории, целиком проходящей внутри батареи: $U_{12} = – I \cdot r $
- Для траектории, целиком проходящей снаружи батареи: $U_{12} = \varphi_1 – \varphi_2 = \mathcal {E}_{bat} – I \cdot r $
Анализ для резистора
В резисторе на условный носитель положительного заряда действуют только две силы, уравновешивающие друг друга:
- $\vec F_{кул}$, связанная с кулоновской компонентой поля $\vec E_{кул}$ внутри резистора,
- $\vec F_{дис}$, связанная с диссипативными силами внутри резистора.
Внутри резистора не действуют внешние силы, и $ \varphi_3 – \varphi_4 = U_{34}$. По закону Ома ток через резистор равен $I = U_{34} / R$, где $R$ – его сопротивление.
Анализ для соединительных проводов
Рассмотрим для примера провод на участке 1-3. В нём протекает ток $I$ и общем случае действуют внешние силы (например, вследствие магнитной индукции). По закону Ома для неоднородного участка $$ I \cdot R_{wire} = \varphi_1 – \varphi_3 + \mathcal {E_{13}} $$
Поскольку сопротивление провода $R_{wire}$ пренебрежимо мало, можно записать, что $$ \varphi_3 – \varphi_1 = \mathcal {E_{13}} $$
Если внешние силы отсутствуют, то такой провод ($R \rightarrow 0$) является эквипотенциальным.
Анализ для силы тока
Проанализируем замкнутую траекторию 1-3-4-2-1, пользуясь свойством потенциальности кулоновского поля (или вторым правилом Кирхгофа).
$$\varphi_{13421} = \varphi_{13} + \varphi_{34} + \varphi_{42} + \varphi_{21} = 0$$
$$\mathcal {E}_{31} + I \cdot R + \mathcal {E}_{24} – \mathcal {E}_{bat} + I \cdot r = 0$$
$$(\mathcal {E}_{31} +\mathcal {E}_{24}) – \mathcal {E}_{bat} + I \cdot ( R + r) = 0$$
$$I = \frac {\mathcal {E}_{bat} – (\mathcal {E}_{31} +\mathcal {E}_{24})} {R+r}$$
В отсутствие внешних сил в проводах это выражение описывает “закон Ома для полной цепи”:
$$I = \frac {\mathcal {E}_{bat}} {R+r}$$
Анализ для вольтметра
Повторим выражение для разности потенциалов между точками 1 и 2, куда подключён вольтметр: $$\varphi_1 – \varphi_2 = \mathcal {E}_{bat} – I \cdot r $$
Подставим в него вычисленное ранее значение тока: $$\varphi_1 – \varphi_2 = \mathcal {E}_{bat} – r \frac {\mathcal {E}_{bat} – (\mathcal {E}_{31} +\mathcal {E}_{24})} {R+r}$$
$$\varphi_1 – \varphi_2 = \mathcal {E}_{bat} \frac {R}{R+r} – (\mathcal {E}_{31} +\mathcal {E}_{24}) \frac {r}{R+r}$$
С учётом малого тока через вольтметр и малого сопротивления проводов вычислим разность потенциалов на клеммах вольтметра, то есть его фактические показания: $$ \varphi_{AB} = \mathcal {E}_{1A} + \varphi_{12} + \mathcal {E}_{B2}$$
$$ \varphi_{AB} = \mathcal {E}_{bat} \frac {R}{R+r} – (\mathcal {E}_{31} +\mathcal {E}_{24}) \frac {r}{R+r} + \mathcal {E}_{1A} + \mathcal {E}_{B2}$$
При отсутствии внешних сил в проводах это выражение сильно упрощается:
$$ \varphi_{AB} = \mathcal {E}_{bat} \frac {R}{R+r} $$
Выводы
Когда через реальную батарею течёт ток, часть энергии преобразуется в тепловую диссипативными силами. Влияние этих сил в стационарном режиме эквивалентно наличию “внутреннего сопротивления”, встроенного последовательно с ЭДС батареи.
Вольтметр в такой цепи (при условии потенциальности внешнего поля) из-за действия диссипативных сил внутри батареи показывает значение, которое меньше её номинального $\mathcal {E}_{bat}$. В общем случае показания включает в себя ЭДС в измерительных проводах, и некоторую часть ЭДС в проводах между батареей и резистором.
В непотенциальном внешнем поле показания вольтметра могут быть непостоянными, и значительно меняться в зависимости от расположения вольтметра и проводов в пространстве. Наиболее заметны такие искажения при измерении малых переменных напряжений, или в присутствии сильных переменных полей вокруг измерительных проводов.
Однородное кольцо в переменном магнитном поле
Представим тонкое кольцо (площадь кольца $S$, длина окружности $l$) из однородного материала с низкой проводимостью $\sigma$, которое находится в однородном и линейно растущем магнитном поле $\vec B$, направленном вдоль его оси. Благодаря низкой проводимости мы можем пренебречь возбуждаемым магнитным полем самоиндукции: ток, протекающий в кольце будет мал, как и возбуждаемое им собственное магнитное поле.
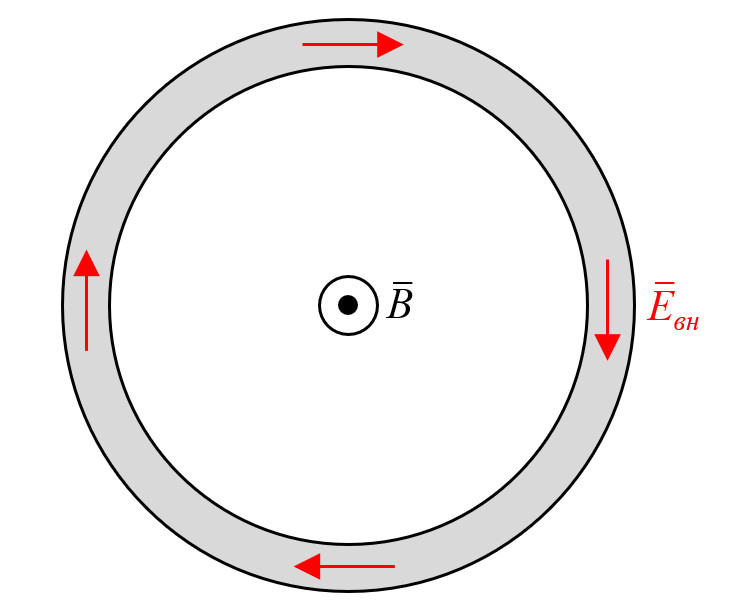
Закон электромагнитной индукции Фарадея (третье уравнение Максвелла в интегральной форме), гласит, что для любого замкнутого контура индуцированная ЭДС равна скорости изменения магнитного потока, проходящего через этот контур, взятой с отрицательным знаком. Согласно этому закону, в кольце возбуждается ЭДС, равная $$ \mathcal {E}_{инд} = – \frac {d \Phi}{dt} = – S \frac {dB}{dt} $$
Действие сил электромагнитной индукции можно представить в виде напряжённости электрического поля $\vec E_{вн}$, существующей внутри кольца и в каждой точке направленной вдоль оси его сечения. Величина этого поля определяется как $$ E_{вн} = \frac {\mathcal {E}_{инд}}{l} = – \frac {S}{l} \frac{dB}{dt} $$
Запишем закон Ома для неоднородного проводника по замкнутому контуру вдоль кольца: $$ IR = \mathcal {E}_{инд} $$
$$ j = \sigma E_{вн} = – \sigma \frac {S}{l} \frac{dB}{dt} $$
Электрическое поле, порождённое движущимися носителями заряда в кольце, стационарно и потенциально (компонента $\vec E_{кул}$). Более того, из-за однородности и симметричности кольца плотность распределения носителей заряда также осесимметрична. Это значит, что разность потенциалов между любыми двумя точками кольца равна нулю, хотя в нём течёт ненулевой ток, а проводимость не бесконечна. Действие внешних сил в каждой точке уравновешивается диссипативными силами.
Незамкнутое кольцо и положение вольтметра
Этот опыт — классическая иллюстрация “парадокса”, в котором показания вольтметра зависят от расположения его проводов в пространстве.
Представим себе незамкнутое кольцо площадью $S$ из хорошего проводника (изображено чёрным цветом), внутри которого существует однородное и линейно растущее магнитное поле $\vec B$, направленном вдоль его оси. Будем считать, что магнитное поле существует только внутри этого кольца.
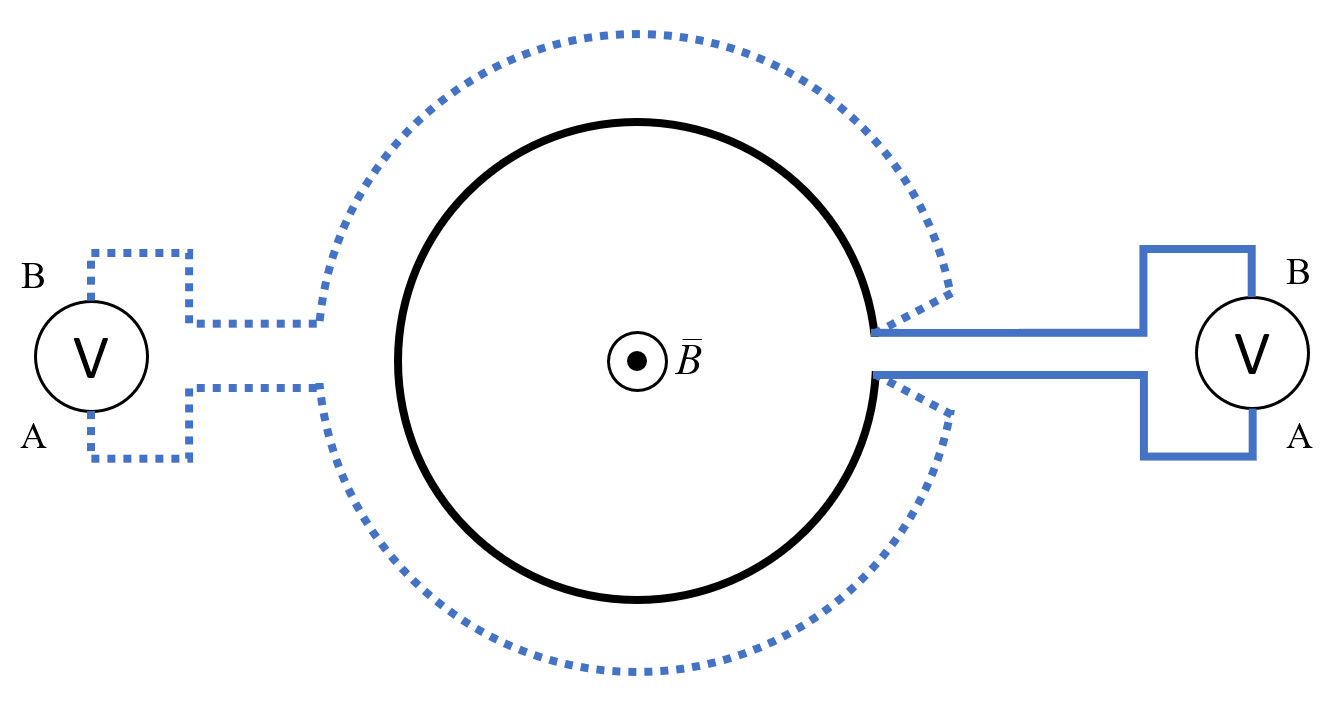
Вольтметр, подключённый к кольцу, может быть расположен в пространстве двумя способами, как показано на рисунке.
Рассмотрим случай, когда вольтметр расположен справа:
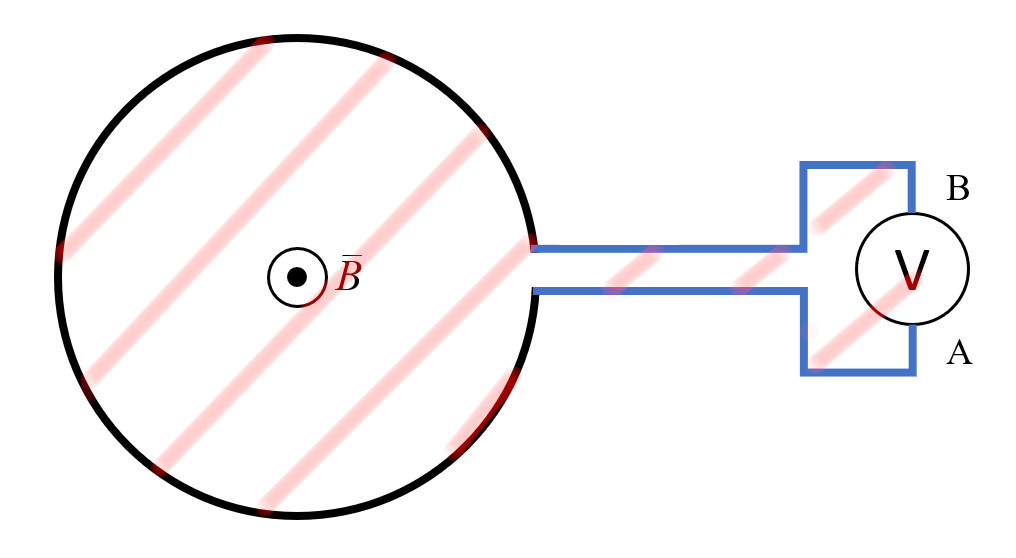
Согласно закону электромагнитной индукции Фарадея, в этом контуре возбуждается ЭДС индукции. Магнитное поле существует (и изменяется) только внутри чёрного кольца, поэтому изменение полного магнитного потока через контур $d \Phi / dt$ равно изменению магнитного потока через кольцо, а ЭДС в контуре равна $ \mathcal {E}_{инд} = S \cdot dB / dt$. Сопротивление вольтметра большое, а значит, ток через него близок к нулю. Запишем закон Ома для неоднородного участка от точки A к точке B по траектории, проходящей через кольцо (внешней для вольтметра), и вычислим разность потенциалов на его клеммах:
$$ 0 = \varphi_A – \varphi_B + \mathcal {E}_{инд}$$
$$ \varphi_{AB} = – \mathcal {E}_{инд}$$
Вольтметр показывает $ – \mathcal {E}_{инд}$
Теперь перенесём вольтметр в левую часть:
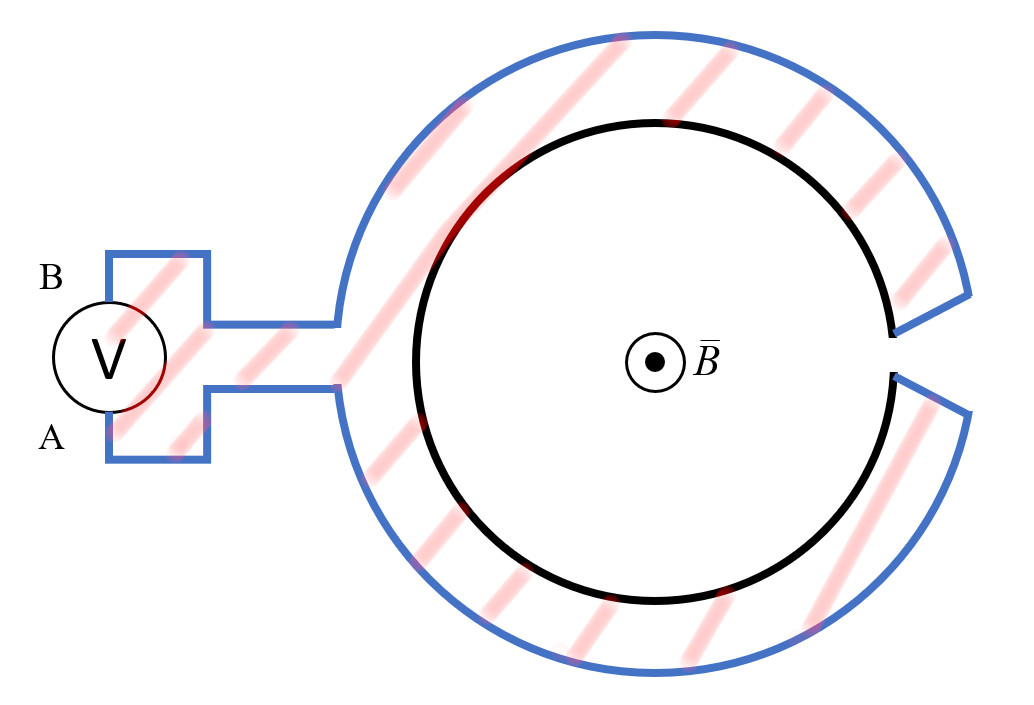
Магнитный поток через замкнутый контур, образованный вольтметром, его проводами и чёрным кольцом, равен нулю: по условию магнитное поле существует только внутри чёрного кольца. Таким образом, ЭДС индукции в этом контуре равна нулю, как и показания вольтметра.
Выводы
В реальном мире показания вольтметра могут зависеть от положения его проводов в пространстве. Закон индукции Фарадея справедлив всегда. Может показаться, что результаты опыта противоречат законам теории цепей, но этот “парадокс” разрешается при использовании модели, учитывающей ЭДС в проводах вольтметра. Такую модель можно построить с использованием связанных индуктивностей, либо просто источников ЭДС.
Примеры корректных эквивалентных моделей, объясняющих этот “парадокс”, приведены ниже.
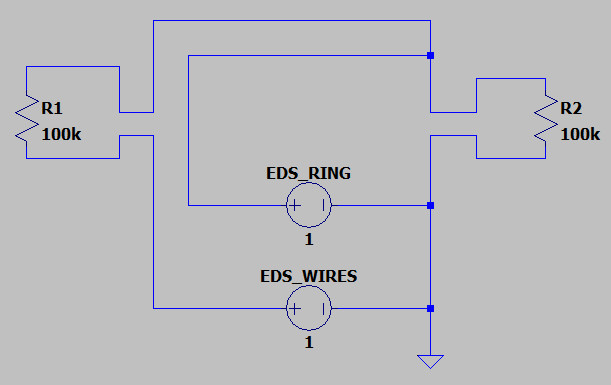
Вольтметры изображены резисторами R1 (левый вольтметр) и R2 (правый)
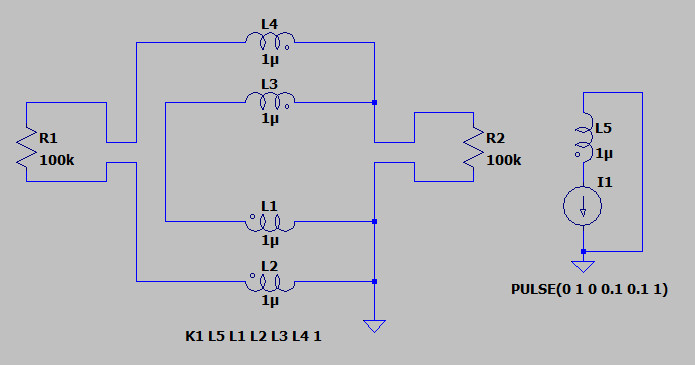
L1, L3 соответствуют чёрному кольцу; L2 и L4 – провода к левому вольтметру, L5 – источник возбуждения
Заключение
Теорию цепей можно и нужно использовать для анализа реальных устройств, имея в виду допущения и ограничения этой теории. При необходимости в модель электрической цепи необходимо добавлять дополнительные элементы, имитирующие свойства реальных проводников и компонентов.
Напряжение и разность потенциалов в физике имеют разный смысл. Величина напряжения в общем случае зависит не только от выбора двух точек, но и от выбора конкретной траектории между ними.
В электронике (схемотехнике, теории цепей) термин “напряжение” чаще всего имеет физический смысл разности потенциалов. Это неверно с точки зрения электродинамики, но так сложилось исторически. Напряжение, падение напряжения, разность потенциалов — всё это в электронике, как правило, означает именно разность потенциалов.
Внешнее электромагнитное поле может влиять на результат измерений, иногда искажая его до неузнаваемости. С этим часто сталкиваются при измерениях в импульсных преобразователях, когда щупы (или измерительные провода) расположены в мощном переменном магнитном поле.
Further reading
- Д. В. Сивухин — Общий курс физики, том 3
- И. В. Савельев — Курс общей физики, том 2
- Герман Хэртэл — Напряжение и поверхностные заряды — перевод статьи о распределении зарядов в проводниках со стационарными токами
- В. С. Малых, И. Н. Жукова. Электрическое напряжение: термин один, понятия — разные
- Energizer. Battery Internal Resistance — очень краткое введение в физикохимическую природу внутреннего сопротивления батареек
- Assis, Hernandes — The Electric Force of a Current — фундаментальная работа, описывающая явления постоянного тока с физической точки зрения
- John W. Belcher — Kirchhoff’s Voltage Law (KVL) and Faraday’s Law — анализ “парадоксов”, возникающих при применении теории электрических цепей к материальному миру (содержит неверное допущение об отсутствии поля $\vec B$ в пространстве за пределами кольца)