TL;DR: оптимизация ширины меандра позволяет избежать отражения около 4% амплитуды (и выше для сильно связанных диффпар) сигнала на каждом шаге меандра. Это важно, когда длина фронта сопоставима с длиной структуры меандра (обычно для 5 Гбит/с и выше).

Если не указано отдельно, далее в статье понятие “импеданс” используется в смысле “мгновенный дифференциальный импеданс, Zdiff”. Более подробно про разные импедансы в диффпаре можно прочитать в презентации, а краткий обзор ниже:

• Zdiff – импеданс диффпары, когда к линии приложен дифф. сигнал. Zdiff = 2*Zodd
• Zodd – импеданс одного проводника, когда к линии приложен дифф. сигнал
• Zeven – импеданс одного проводника, когда к линии приложен синфазный сигнал
• Zcomm – импеданс диффпары, когда к линии приложен синфазный сигнал. Zcomm = Zeven/2

Почему важен постоянный импеданс

Любая волна отражается при изменении волнового сопротивления – и свет, и радио, и сигнал на печатной плате. Коэффициент отражения зависит от разницы волновых сопротивлений на границе сред. Если импеданс дифференциальной пары изменяется, отражённая часть сигнала будет распространяться в обратном направлении. Это плохо, потому что полученный сигнал на стороне приёмника будет ослаблен (так как часть энергии отражена обратно к передатчику) и искажён из-за множественных отражений от неоднородностей и источника. В предельном случае это приводит к “закрытому глазу” (нулевое раскрытие глазковой диаграммы) и невозможности декодировать сигнал на стороне приёмника.

Почему нужно выравнивать длину внутри диффпары

Сигналы в дифференциальной паре могут распространяться в двух основных режимах: синфазном (even mode) и противофазном (odd mode). Нам наиболее интересен противофазный, при котором в каждый момент времени падающий фронт на одной линии совпадает с растущим фронтом на другой.

Когда падающий и растущий фронты “разбегаются” между собой, часть дифференциального сигнала становится синфазным. На стороне приёмника это приводит к искажению сигнала и росту синфазного шума. Основные причины для разбега фаз – ассиметрия среды (в том числе glass fiber weave effect) и разница длин проводников.

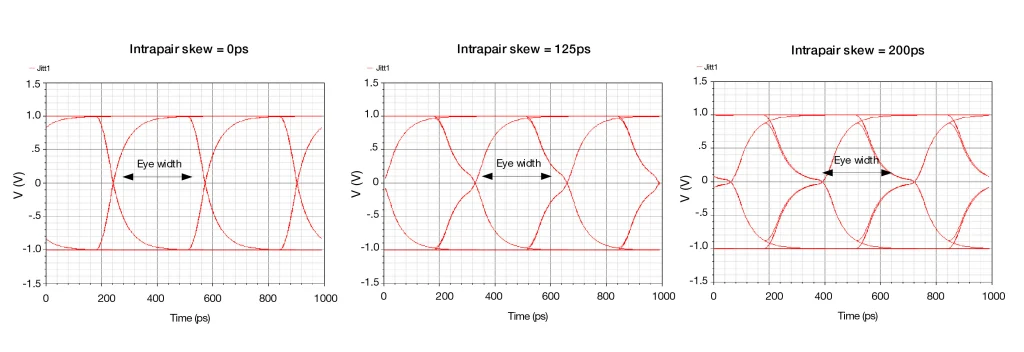
Какая разница длин допустима

Скорость, с которой распространяется сигнал, определяется свойствами среды, в которой изменяется электромагнитное поле. В вакууме это скорость света, а в любой другой среде – медленнее в sqrt(epsilon*mu) раз. Поскольку магнитная постоянная mu для материалов печатной платы равна единице, про неё можно забыть, и работать только с epsilon.

Среда часто бывает неоднородной, поэтому для удобства расчетов используют понятие эффективной диэлектрической постоянной. На внутренних слоях (stripline) электрическое поле целиком сосредоточено в диэлектрике, и эффективное значение равно epsilon диэлектрика печатной платы. На внешних слоях (microstrip) часть электрического поля распространяется в воздухе, а часть в диэлектрике, поэтому эффективное значение – что-то среднее между epsilon воздуха и диэлектрика печатной платы. Распределение поля между воздухом и диэлектриком в синфазном и дифференциальных режимах для microstrip отличается, поэтому скорость распространения сигнала в odd и even mode тоже немного разная.

На внешнем слое печатной платы дифференциальный сигнал проходит 1 мм за ~5.6 пикосекунд (примерно в 1.7 раза медленнее, чем в воздухе).

Для примера вычислим допустимый сдвиг фаз для некоторого цифрового сигнала, опираясь на его битрейт. USB 3.2 Gen1 имеет битрейт 5 Гбит/с, и его фундаментальная частота равна 2.5 ГГц (это первая гармоника сигнала 101010…10). Если наш трансивер быстрый и мощный, важные составляющие сигнала могут простираться вплоть до пятой-седьмой гармоники. Ограничимся пятой: 12.5 ГГц. Длина волны на этой частоте в воздухе составляет 24 мм, а в дорожке на внешнем слое печатной платы – около 14 мм. Традиционно считают, что проблемы начинаются при сдвиге от 1/10 длины волны. Таким образом, для 5 Гбит/с теоретически допустима разница длин до 1.4 мм.

Пятая гармоника – хорошая оценка сверху, но в стандартных материалах печатных плат (mid-loss, tan=0.02) высокие гармоники довольно быстро затухают. Это приводит к завалу фронтов сигналов и закрытию глаза. Суммарные потери в линии за счет диэлектрика, меди и шероховатости составят примерно 0.14 дБ на дюйм-ГГц линии, то есть:

• на 12.5 ГГц (пятая гармоника 5 Гбит/с) – примерно 1.7 дБ/дюйм,
• на 7.5 ГГц (третья гармоника) – 1 дБ/дюйм,
• на 2.5 ГГц (фундаментальная частота) – 0.35 дБ/дюйм.

Если ориентироваться на третью гармонику 5 Гбит/с, получим допуск в 2.3 мм.

На практике дополнительный вклад вносит неидеальность передатчика (выходной сигнал не строго противофазен), неидеальность приёмника (он тоже не строго дифференциален), неоднородности среды (в том числе fiber weave) и некоторые другие факторы, так что имеет смысл минимизировать разницу длин настолько, насколько это возможно.

Как выравнивать длину

Существуют два основных подхода: “меандр” и “тромбон”.

Меандр – небольшие изгибы одного из проводников, которые приводят к увеличению его геометрической длины. Применяется, когда разница длин сравнительно небольшая. Дальше мы будем говорить про детали его реализации.

Тромбон – изгиб в виде петли, позволяющий исправить очень большую разницу длин. Обычно применяется для single-ended линий (DDR), а не для исправления skew внутри дифференциальной пары. Внутри тромбона связь между линиями диффпары отсутствует, поэтому это решение плохо подходит для сильно связанных дифференциальных пар.

Проблемы с меандром

Основные проблемы, которые можно получить при выравнивании длины меандром – паразитная емкостная и индуктивная связь между “выступами” и неоднородности дифференциального импеданса.

Паразитная связь

Чтобы избежать избыточной связи между сегментами, придерживайтесь больших зазоров: не менее четырех-пятикратной ширины линии (5*W) и выше.

Неоднородность импеданса

Вторая проблема заключается в локальных изменениях дифференциального импеданса: когда мы увеличиваем зазор между проводниками дифференциальной пары, её импеданс возрастает. Этот эффект очень заметен для сильно связанных дифференциальных пар.

Чтобы компенсировать это изменение, предлагается увеличивать ширину проводников на этих участках – либо только на стороне меандра (“Good”), либо симметрично (“Better”):

Количественная оценка изменения импеданса на меандре

Для примера возьмем стек с толщиной диэлектрика 0.12 мм, часто встречающийся у производителей, и оценим влияние меандра на импеданс дифференциальной пары на внешнем слое (microstrip) с сильной связью. Целевым значением импеданса выберем 90 Ом (USB3).

Расчетная ширина проводника W	0.2 mm
Зазор между проводниками S	0.21 mm
Зазор между проводниками в меандре Sm	0.56 mm
Высота над опорным слоем H	0.12 mm
Диэлектрическая постоянная Er	4.4
Ширина проводника с учетом подтрава	0.1 мм
Суммарная толщина меди на внешнем слое	35 мкм

Дифференциальный импеданс такой линии составляет 90.37 Ом. В процессе выравнивания зазор увеличивается до 0.56 мм, а дифф. импеданс возрастает до 97.51 Ом (отклонение на 7.9 %). Каждое подобное изменение импеданса приведет к отражению части сигнала (около 3.8% по амплитуде). Это достаточно много, чтобы усугубить имеющиеся проблемы или добавить новые.

Чтобы повысить однородность импеданса в меандре, увеличим ширину дорожек на участках с большим зазором. Для нашего примера (зазор 0.56 мм) требуемая ширина составит 0.23 мм. На глаз изменение почти не заметно, но оказывает значимое влияние на качество сигнала.

Также имеет смысл сгладить переход между разными толщинами, как это продемонстрировано в аппноте от Intel (предыдущая картинка).

Сильная или слабая связь?

Влияние меандра на изменение импеданса зависит от того, насколько велика связь между двумя проводниками диффпары. Чем ближе линии друг к другу, и чем дальше они от опорного слоя, тем связь сильнее. На картинке изображены: слева – сильно связанная (strong coupling) диффпара, справа – слабосвязанная (weak coupling).

Оба подхода имеют свои плюсы и минусы. Если не гнаться за максимальной плотностью трассировки (количество диффпар на единицу площади печатной платы), слабая связь более предпочтительна. Специальный случай – отсутствие опорного слоя, тогда имеет смысл использовать сильную связь (но на печатной плате это большая редкость).

Плюсы слабой связи

Плюсы сильной связи

– Расстояние между линиями слабо влияет на импеданс: проще переходить между слоями, выравнивать длину, проходить через pin/via field – Не критично выравнивать длину внутри каждого сегмента – При необходимости проводники можно вести как single-ended – Как правило, меньше перекрёстные помехи (это неочевидно) – Меньше потерь сигнала (так как ширина линии больше) – Позволяет использовать более тонкий диэлектрик (это важно, когда слоёв печатной платы очень много)

– Повышенная плотность трассировки – Меньшая зависимость от опорного слоя

Как понять, слабая или сильная связь внутри диффпары? Можно сравнить Zeven и Zodd в солвере, либо оценить изменение Zdiff при вариации зазора между проводниками. Если Zdiff почти не зависит от зазора, значит, диффпара слабосвязанная.

Routing Topology	Dielectric Constant (Er)	Trace Width (W)	Trace Separation (S)	Height above reference plane (H)	Zdiff (Ω)
Loosely coupled microstrip	3.7	6 mils (=0.15 мм)	12 mils (2*W)	4 mils (=0.1 мм)	100
Loosely coupled microstrip, S++	3.7	6 mils	18 mils (3*W)	4 mils	102
Tightly coupled microstrip	3.7	6 mils	6 mils (1*W)	4.8 mils (=0.12 мм)	100
Tightly coupled microstrip, S++	3.7	6 mils	12 mils (2*W)	4.8 mils	112

В этом примере увеличение зазора на одну ширину линии меняет импеданс слабосвязанной диффпары на 2 Ома. Для сильно связанной дифференциальной пары такое же увеличение зазора увеличивает импеданс на 12 Ом (в шесть раз сильнее).

Инструменты САПР

Современные eCAD (Altium Designer, Cadence Allegro) имеют встроенные инструменты для выравнивания длин проводников дифференциальных пар, но не реализуют компенсацию изменений импеданса.

Удобнее всего работать со слабосвязанными диффпарами, для которых компенсация не нужна, но если в вашем дизайне есть диффпары с сильной связью – придётся оптимизировать руками.

Further reading

1. Статья Intel о выравнивании внутри диффпары и компенсации импеданса
2. Презентация Eric Bogatin о том, как устроена диффпара, что такое Zodd и Zeven
3. Статья DesignCon 2019 о хитрых методах уменьшения skew
4. Рекомендации Intel о высокоскоростном роутинге
5. Статья Eric Bogatin о влиянии связи внутри диффпары на crosstalk
6. Презентация Broadcom со сравнением сильной и слабой связи в диффпарах
7. Аппнота Intel о сравнении сильной и слабой связи в диффпарах
8. Статья от Maxim Integrated о частотной зависимости skew и влиянии на качество сигнала